25/2/04 Example 5 The level curves of f(x,y) = x 2 y 2 are curves of the form x 2 y 2 =c for different choices of c These are circles of radius square root of c Several of them are shown below One can think of the level curve f(x,y)=c as theNeed to translate "LEVEL CURVES" from english and use correctly in a sentence?Level curves and contour plots are another way of visualizing functions of two variables If you have seen a topographic map then you have seen a contour plot Example To illustrate this we first draw the graph of z = x2 y2 On this graph we draw contours, which are curves at a fixed height z = constant For example the curve at height z = 1 is the circle x2 y2 = 1
Level Curves And Contour Plots Mathonline
What are level curves
What are level curves-The level curves of $f(x,y)$ are curves in the $xy$plane along which $f$ has a constant value The level surfaces of $f(x,y,z)$ are surfaces in $xyz$space on which $f$ has a constant value Sometimes, level curves or surfaces are referred to as level sets In this Photo Editing tutorial, we'll look at the similarities between two of Photoshop's most important image editing tools the Levels and Curves adjustments At first glance, the Curves adjustment may seem less like an image editing tool and more like something only a scientist would know what to do with, especially when compared with the much simpler Levels



Section 13 1 Level Curves Youtube
Level Curves and Surfaces Example 1 In mathematics, a level set of a function f is a set of points whose images under f form a level surface, ie a surface such that every tangent plane to the surface at a point of the set is parallel to the level setLevel curves, or contours, are the curves corresponding to the equation f(x,y)=h for various fixed values of the elevation z=h For example on a topopmap they might be traced for every etc) Often a thicker line is used for every21/1/ A level curve of a function f(x,y) is the curve of points (x,y) where f(x,y) is some constant value A level curve is simply a cross section of the graph of z=f(x,y) taken at a constant value, say z=c A function has many level curves, as one obtains a different level curve for each value of c in the range of f(x,y)
25/3/21 The level curves of are curves in the plane along which has a constant value The level surfaces of are surfaces in space on which has a constant value Sometimes, level curves or surfaces are referred to as level setsIe the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is theLEVEL CURVES The level curves (or contour lines) of a surface are paths along which the values of z = f(x,y) are constant; The level curves are shown in Figure 124(a) Note how the level curves for \(c=0\) and \(c=02\) are very, very close together this indicates that \(f\) is growing rapidly along those curves Figure \(\PageIndex{4}\) Graphing the level curves in Example 1214 In Figure \(\PageIndex{4b}\), the curves are drawn on a graph of \(f\) in space
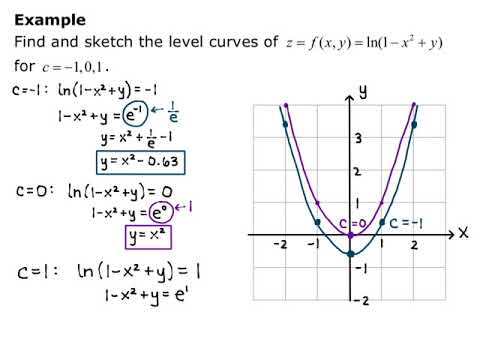
For example, if c = − 1, the level curve is the graph of x 2 2 y 2 = 1 In the level curve plot of f (x, y) shown below, the smallest ellipse in the center is when c = − 1 Working outward, the level curves are for c = − 2, − 3, , − 10We discuss level curves what are they, how do you find them, and what do they look like?Read about Level Curves referenceor see Level Curves Grapher 21 plus Level Curves Calc 3 Level Curves Calc 3 level curves calc 3 Learn more Level Curves reference pic Pic Problem On Surfaces And Level Curves Leading Lesson pic Pic Level Set Examples Math Insight pic




Level Curves Examples




Level Sets Math Insight
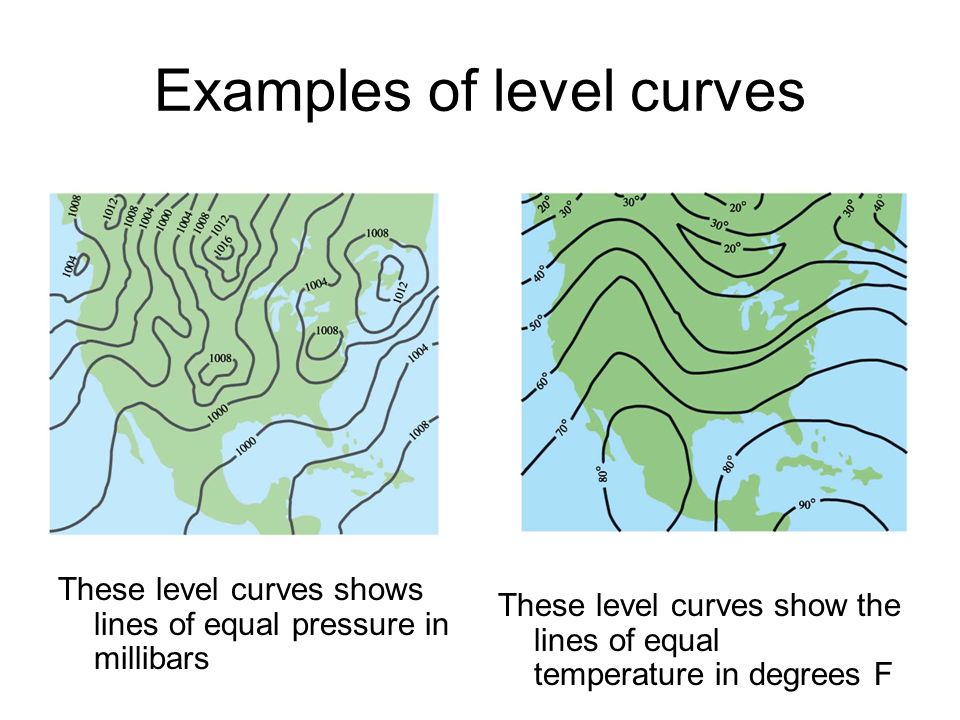
One common example of level curves occurs in topographic maps of mountainous regions, such as the map in Figure 2 The level curves are curves of constant elevation of the Gran canyon Notice that if you walk along one of these contour lines you neither ascend nor descend Figure 2 Gran Canyon topographic mapHere is an example to understand the indifference curve better Peter has 1 unit of food and 12 units of clothing Now, we ask Peter how many units of clothing is he willing to give up in exchange for an additional unit of food so that his level of satisfaction remains unchangedPython input_outputlevel_curves examples Here are the examples of the python api input_outputlevel_curves taken from open source projects By voting up you can indicate which examples are most useful and appropriate 1 Examples 3 Source File curvepy, under MIT License, by jeanfeydy @staticmethod




Calculus Iii Functions Of Several Variables



The Gradient And Directional Derivative
Level Curves Def If f is a function of two variables with domain D, then the graph of f is {(x,y,z) ∈ R3 z = f(x,y) } for (x,y) ∈ D Def The level curves of a function f(x,y)are the curves in the plane with equations f(x,y)= kwhere is a constant in the range of f The contour curves are the corresponding curves on the surface, the intersection of the24/7/21 Type D MCB Dcurve devices are suitable for applications where high levels of inrush current are expected The high magnetic trip point prevents nuisance tripping in high inductive applications such as motors, transformers, and power supplies Method Of Types What is level curvesLevel sets show up in many applications, often under different names For example, an implicit curve is a level curve, which is considered independently of its neighbor curves, emphasizing that such a curve is defined by an implicit equationAnalogously, a level surface is sometimes called an implicit surface or an isosurface The name isocontour is also used, which means a contour of



Examples Wednesday Feb 19




Applicable Mathematics 2 Examples 1 Level Curves
Level Curves and Surfaces Example 2 In mathematics, a level set of a function f is a set of points whose images under f form a level surface, ie a surface such that every tangent plane to the surface at a point of the set is parallel to the level setThe graph itself is drawn in an ( x, y, z) coordinate system Remark 2 Level curves of the same function with different values cannot intersect Remark 3 Level curves of utility functions are called indifference curvesHigh quality example sentences with "levels curves" in context from reliable sources Ludwig is the linguistic search engine that helps you to write better in English




Some Examples Of Graphs Used In The Problems A Level Curves Of A Download Scientific Diagram




Sketch The Level Curves For F X Y 2x 2 4y 2 Chegg Com
5 Plot the level curves by adding a 2D Graph page to the document and plotting the lists as f1(x)and f2(x) Modify the colors of the level curves if desired The examples use the color green for positive values of z, blue for z = 0, and orange for negative values of z 6 Use the Settings Settings dialog to hide the plot labels 7In your last example, if $z$ is constant then so is $x^2y^2$ This should look familiar, as the level curves for that are hyperbolas If you want to improve, first get comfortable with the conic sections (points, lines, double lines, circles, ellipses, parabolas, and hyperbolas) You could then move on to more complicated onesExamples involving the geometric form of level curves of harmonic functions A Acker, Department of Mathematics Iowa State University Ames, Iowa USA Search for more papers by this author L Payne, In the xy plane, we give, for example, a Jordan curve Γ containing exactly one local maximum and one local minimum in the y
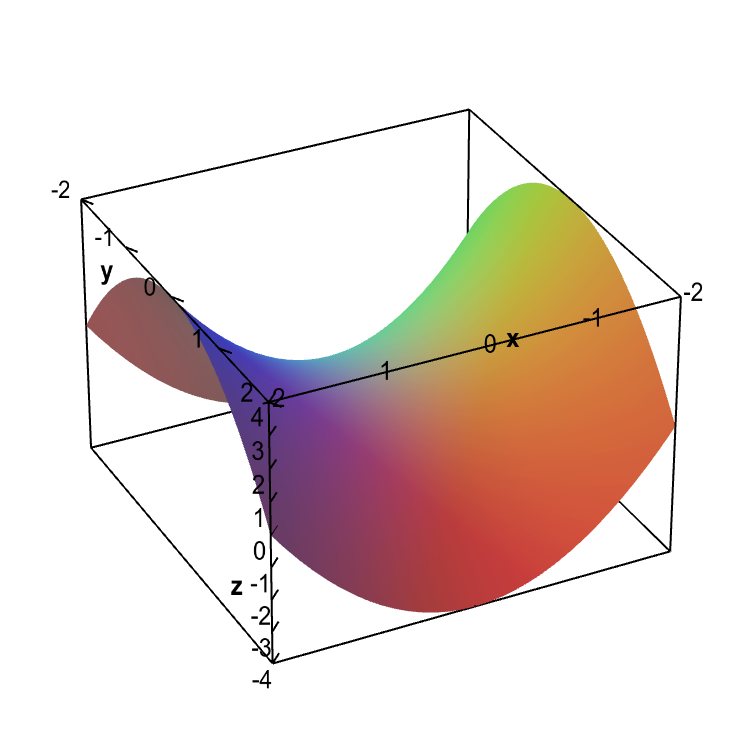



Level Set Examples Math Insight



Functions Of Several Variables Ximera
Curves in R2 Graphs vs Level Sets Graphs (y= f(x)) The graph of f R !R is f(x;y) 2R2 jy= f(x)g Example When we say \the curve y= x2," we really mean \The graph of the function f(x) = x2"That is, we mean the set f(x;y) 2R2 jy= x2g Level Sets (F(x;y) = c) The level set of F R2!R at height cis f(x;y) 2R2 jF(x;y) = cg Example When we say \the curve x 2 y = 1," we really mean \TheOther examples of level curves are isobars and isotherms An isobar is a planar curve where the atmospheric pressure is constant An isotherm is a planar curve along which the temperature is constant De nition 3 (Potential) The function U(x;y) in a conservation law is called a potential The dynamical equation is the rst order di erential equationAnother example is the two variable realvalued function $f(x, y) = x^2 y^2$ which represents a hyperboloid The level curves generated by the planes $z = 1$, $z = 2$, and $z = 3$ are hyperbolas The image below depicts the level curve of this hyperboloid corresponding to $z = 1$



S0 3




How To Sketch Graphs For Functions Of Two Variables Chris Tisdell Unsw Youtube
Level Curves and Surfaces The graph of a function of two variables is a surface in space Pieces of graphs can be plotted with Maple using the command plot3dFor example, to plot the portion of the graph of the function f(x,y)=x 2 y 2 corresponding to x between 2 and 2 and y between 2 and 2, type > with (plots);7/6/21 1 27 27 2k ?Ie the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below isLevel curves are always graphed in the x yplane, x yplane, but as their name implies, vertical traces are graphed in the x z x z or y zplanes y zplanes Definition Consider a function z = f ( x , y ) z = f ( x , y ) withLevel Curves and Surfaces Example 3 In mathematics, a level set of a function f is a set of points whose images under f form a level surface, ie a surface such that every tangent plane to the surface at a point of the set is parallel to the level set



2



Www Usna Edu Users Math Uhan Sm223 Lessons 12 level curves Pdf
Traducciones en contexto de "the level curves" en inglésespañol de Reverso Context The building expresses his condition of extracted local topography noticing the character of support of the wrought ones that are accumulated as untid plates following the level curvesFor example, "tallest building" Search for wildcards or unknown words Put a * in your word or phrase where you want to leave a placeholder For example, "largest * in the world" Search within a range of numbers Put between two numbers For example, camera $50$100 Combine searches Put "OR" between each search query For example, marathonIe the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves of the function Sliding the slider will vary a from a = 1 to a = 1




Calculus Iii Functions Of Several Variables
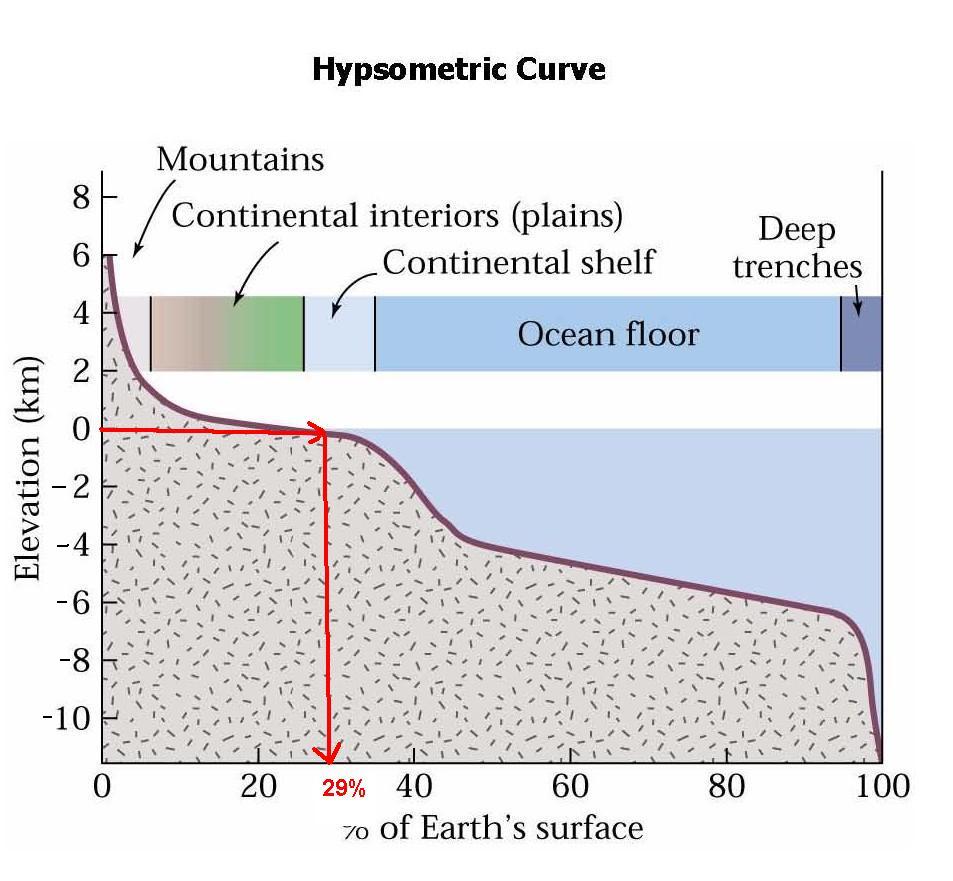



Hypsometric Curve
Here are many translated example sentences containing "LEVEL CURVES" englishspanish translations and search engine for english translations26/5/ The level curves (or contour curves) for this surface are given by the equation are found by substituting \(z = k\) In the case of our example this is, \k = \sqrt {{x^2} {y^2}} \hspace{025in}\hspace{025in} \Rightarrow \hspace{025in}\hspace{025in}{x^2} {y^2} = {k^2}\Level Curves Examples Done in Mathematica Last modified Spring 14




Level Sets Math Insight




Graphs Types Examples Functions Video Lesson Transcript Study Com
Level structures on elliptic curves Classically, level structures on elliptic curves = / are given by a lattice containing the defining lattice of the variety From the moduli theory of elliptic curves, all such lattices can be described as the lattice for in the upperhalf plane Then, the lattice generated by /, / gives a lattice which contains all torsion points on the elliptic curveLevel curves allow to visualize functions of two variables f(x,y) Example For f(x,y) = x2 − y2 the set x2 − y2 = 0 is the union of the lines x = y and x = −y The set x2 − y2 = 1 consists of two hyperbola with with their "noses" at the point (−1,0) and (1,0) The set x2 − y2 = −1 consists of two hyperbola with their noses at (0,1) and (0,−1) Drawing several contour curves {f(x,y) = c }Remark 1 Level curves of a function of two variables can be drawn in an ( x, y) coordinate system;




8 Calculus Of Several Variables U Functions Of



1
F ( x, y) = e − x y and I'm supposed to sketch the level curves f (x,y) = 1, f (x,y) = 3, f (x,y) = 5 I can't post screenshots on here for some reason, so I'll just describe what the graphs look like The solution to this problem says that the level curves would look like an e x graph, but I assumed that the level curves would curve upwardsLevel Curves give me the function f (x,y) Give me a value of Z 4 3 2 1 0 1 2 3 4 Give me another function f (f,y) Give me another value of Z 4 3 2 1 0 1 2 3 4Example 1 Sketch the gradient, and use that to draw the level curves, of the function ( ) We begin by finding the gradient 〈 〉 Since the function is explicit, we need only concern ourselves here with the derivatives for x and y At this point, we could choose a series of points that mark out a grid for our plane and begin to draw




How To Sketch Level Curves Youtube




Level Curves Example 1
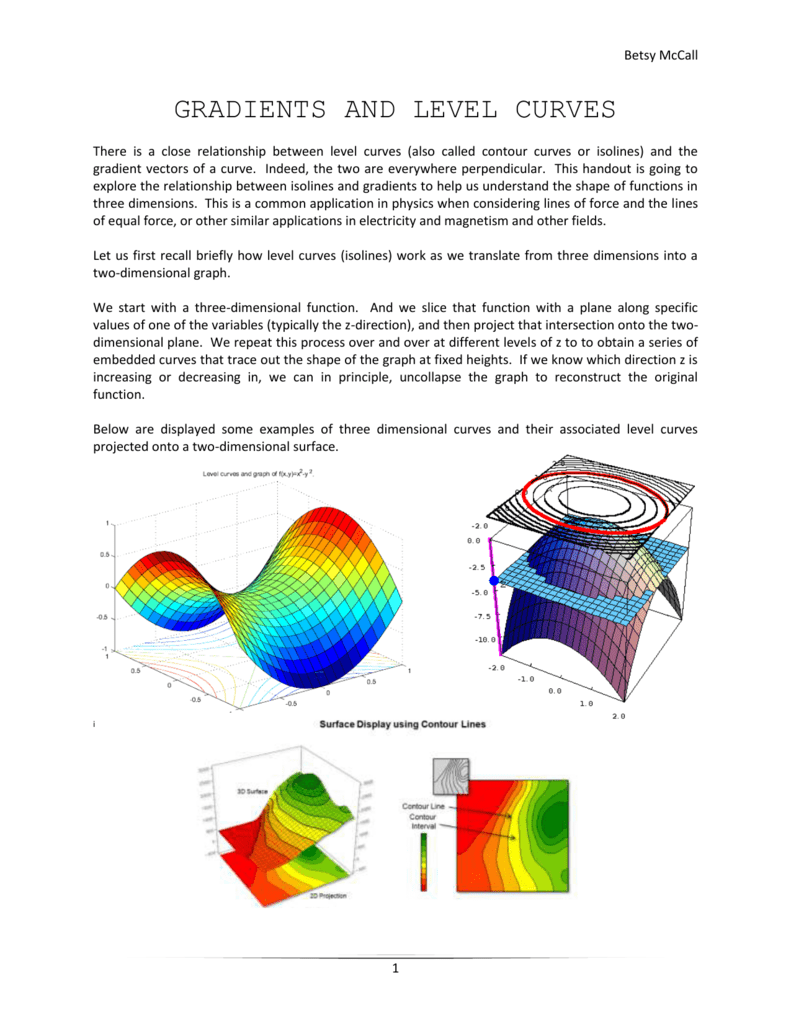



Gradients Level Curves




Section 13 1 Level Curves Youtube



S0 3




In Calculus I And Ii We Worked With Functions Chegg Com




Announcements Topics To Do Ppt Download




Level Curves




Math 2110 Section 13 1 Level Curves And Level Surfaces Youtube




Fun Math Art Pictures Benice Equation Scilab Example Plotting Implicit Curves Level Curves




Level Curves Example 1




Level Curves




Level Set Wikipedia




Level Curves Examples Level Surface



Level Curves And Contour Plots Mathonline



Extra Explanation Wiskunde Op Tilburg University




Subimages And Level Curves For The Image Examples In Fig 8 Download Scientific Diagram




Level Curves Examples




3 Points Writing Prompt 1 Typed 100 0 Words In Chegg Com




Solved Multivariable Functions And Level Curvesi M Having Chegg Com



How To Find The Level Curves Of F X Y Ln Y X 2 Youtube



Pdf A Fast Iterative Method For Eikonal Equations Semantic Scholar
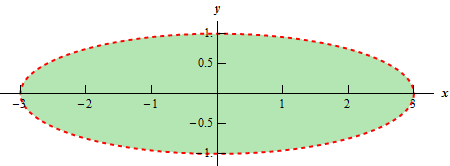



Calculus Iii Functions Of Several Variables



1




Introduction To Functions Of Several Variables Ppt Download



Www Usna Edu Users Math Uhan Sm223 Lessons 12 level curves Pdf
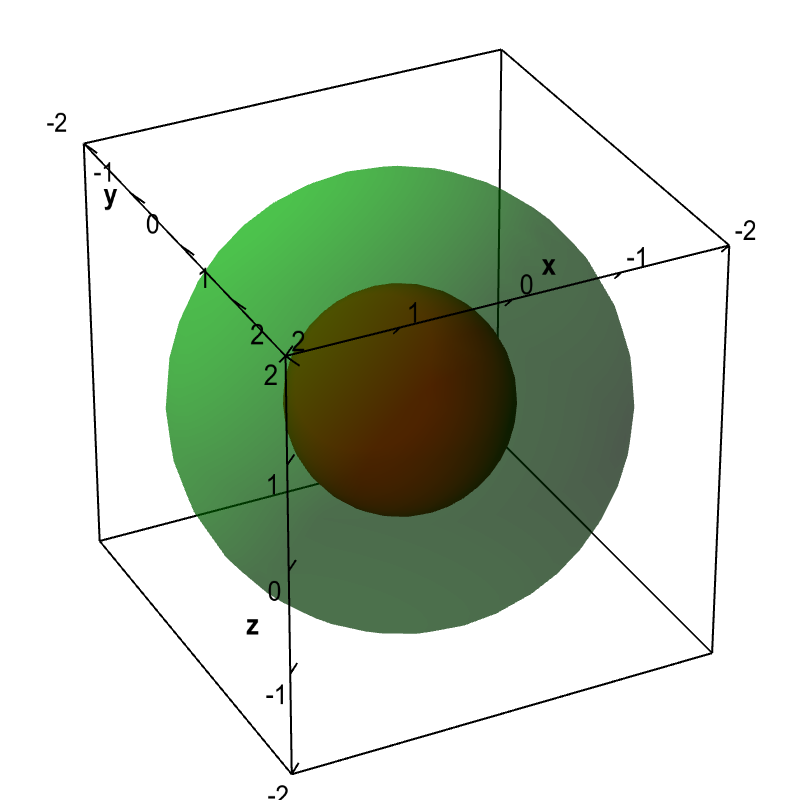



Level Set Examples Math Insight




Level Curves Examples Level Surface



Level Curves And Contour Plots Mathonline




Level Sets Math Insight



1



S0 3




Level Set Wikipedia




Level Curves Examples Level Surface




How To Find The Level Curves Of A Function Calculus 3 Youtube
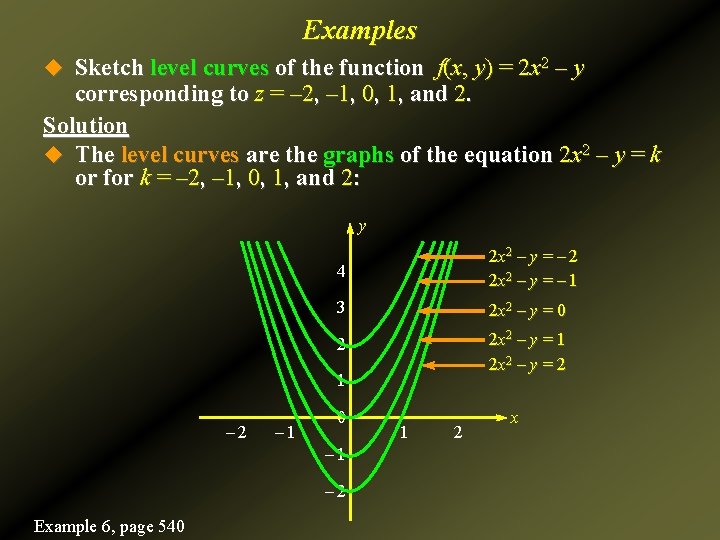



8 Calculus Of Several Variables U Functions Of



Math 225 Calculus Iii
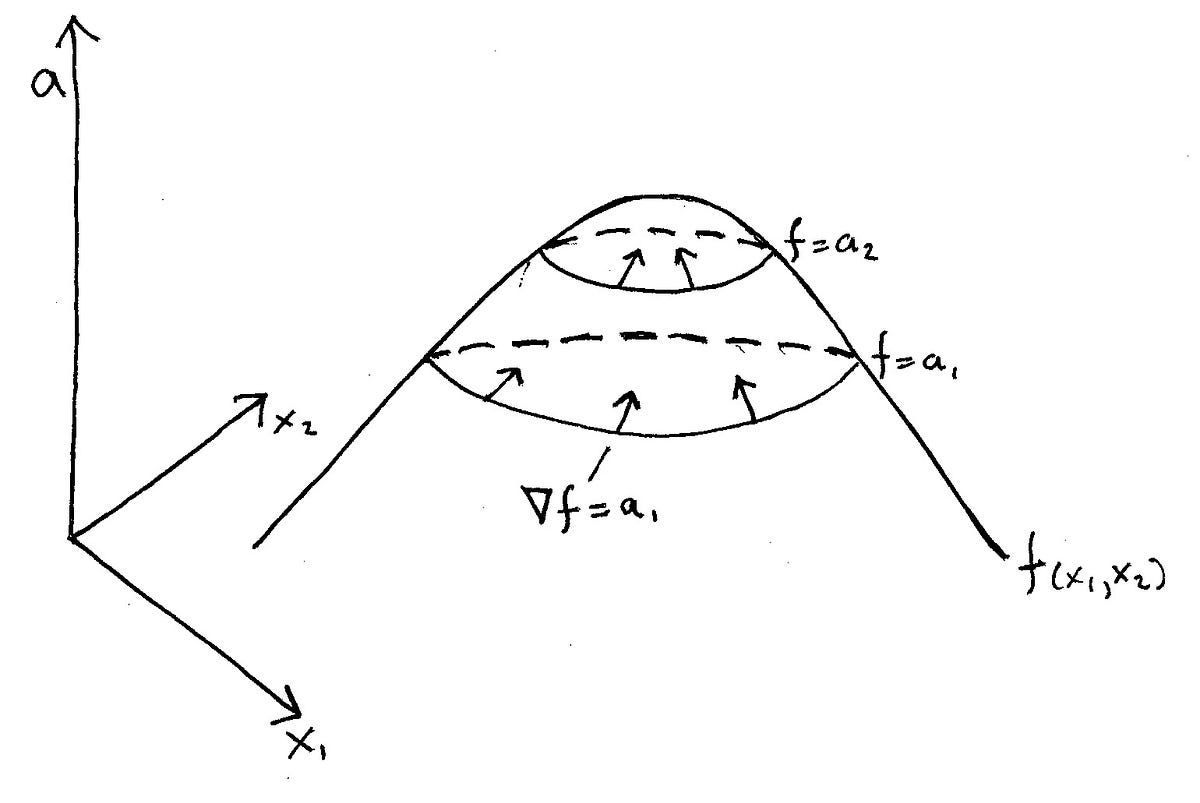



A Simple Explanation Of Why Lagrange Multipliers Works By Andrew Chamberlain Ph D Medium



2
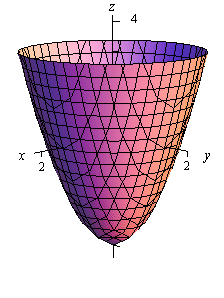



Calculus Iii Functions Of Several Variables
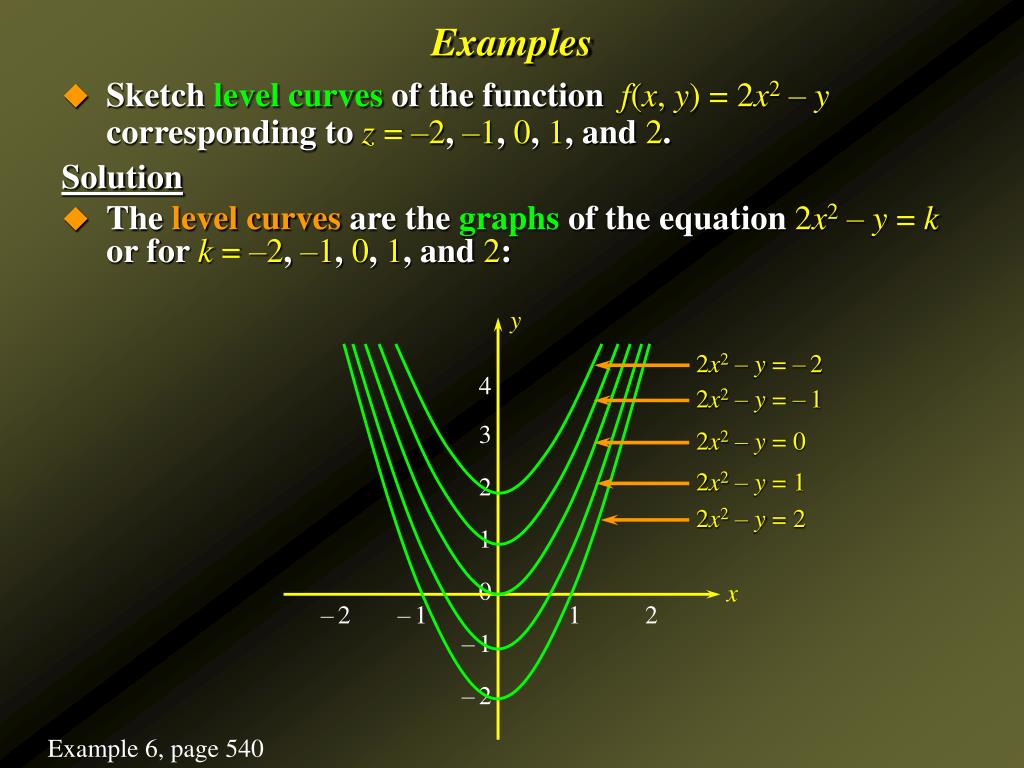



Ppt Functions Of Several Variables Partial Derivatives Powerpoint Presentation Id



12 1 Introduction To Multivariable Functions Mathematics Libretexts




Graphs And Level Curves




Level Set Examples Math Insight



13 1 Day 2 Level Curves Level Curves One Way To Visualize A Function Of Two Variables Is To Use A Scalar Field In Which The Scalar Z F X Y Is Assigned




Calculus Iii Functions Of Several Variables
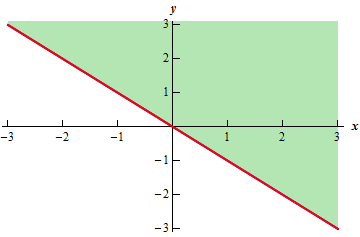



Calculus Iii Functions Of Several Variables




Level Curves Examples Done In Mathematica Last Modified Spring 14




Level Curves Examples Done In Mathematica Last Modified Spring 14




Finding A Function With Level Curves Mathematics Stack Exchange




Calculus Iii Functions Of Several Variables




How To Read A Sea Level Curve Geological Digressions



Level Sets Math Insight



2




Level Set Wikipedia




Level Curves Of Functions Of Two Variables Youtube




Level Curves Of Function At Z 0 Mathematics Stack Exchange



Functions Of Several Variables Ximera



Http Www Ams Sunysb Edu Jiao Teaching Ams261 Fall12 Lectures Larcalc9 Ch13 Pdf




Level Curves



Level Curves And Contour Plots Mathonline



Math 225 Calculus Iii



1




Lesson 15 Gradients And Level Curves



Level Curves And Contour Plots Mathonline




Two Examples Of Eustatic Sea Level Curves That Show Significant Download Scientific Diagram



S0 3




Applicable Mathematics 2 Examples 1 Level Curves




Level Set Wikipedia




Examples Of Two Relative Sea Level Curves From The Disko Bugt Area The Download Scientific Diagram




Topographical Maps Are Examples Of Graphs Using Level Chegg Com




Level Curves Examples




Saddle Point Wikipedia




Level Curves Calculus




Level Curves Examples Done In Mathematica Last Modified Spring 14




Introduction To Functions Of Several Variables




Some Examples Of Graphs Used In The Problems A Level Curves Of A Download Scientific Diagram




3 Points Writing Prompt Typed 100 0 Words In Chegg Com
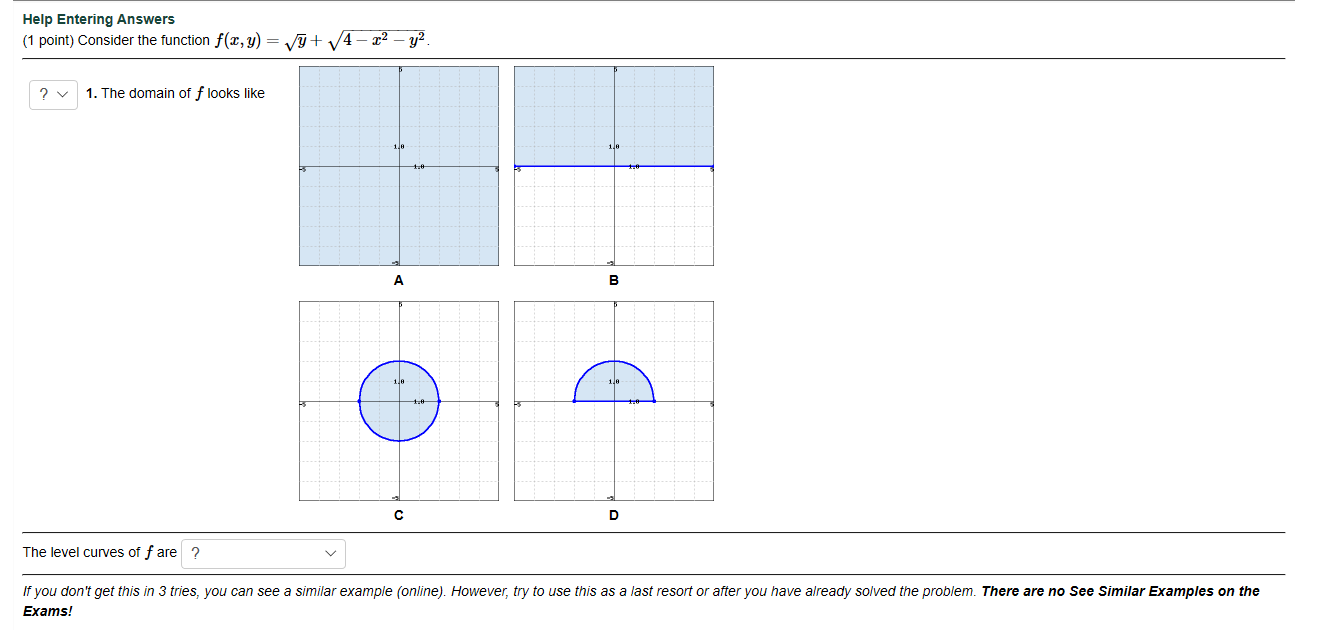



Help Entering Answers 1 Point Consider The Function Chegg Com




Level Curves Examples Level Surface




Level Set Examples Math Insight




Matb41h3 Midterm Detailed Examples For Drawing Level Curves Oneclass



Math 225 Calculus Iii




Subimages And Level Curves For The Image Examples In Fig 8 Download Scientific Diagram



0 件のコメント:
コメントを投稿